SHA256 詳解

在開始深入解釋SHA256 前, 需要為大家說明一下電腦運算的基本智識。

Bit/Byte/Word

Bit(位元): 一個長度為1的二進制數字, 一個bit的值可以為0或1

Byte(位元組): 一個Byte由八個bit組成, 亦可理解成一個8位長的二進制數字。

例如 11001100, 00001111, 01010101
最小的值是00000000 (即十進制的0), 最大值是11111111 (即十進制中的2^8-1 = 255)

一個Byte從右至左每個bit分別代表十進制的1,2,4,8,16,32,64,128

Word(字節): 一個Word由32個bit組成

二進制與十六進制

在下面的例子裏, 同一個數左邊用二進制表示, 右邊用十進制表示:

00000001 = 1 (2的0次方)
00000010 = 2 (2的1次方)
00000100 = 4 (2的2次方)
00001000 = 8 (2的3次方)
00010000 = 16 (2的4次方)
00100000 = 32 (2的5次方)
01000000 = 64 (2的6次方)
10000000 = 128 (2的7次方)

所以, 00000101 如果用十進制來表示, 就是1+4=5。
因為第1個bit和第3個bit是1, 而它們分別代表十進制中的1和4。

要看這一大串0和1很煩吧, 所以很多時電腦科學家會用16進制來表示。

以下是十進制中0-15用二進制/十六進制表示出來的方法:
0000=0x00 0100=0x04 1000=0x08 1100=0x0C
0001=0x01 0101=0x05 1001=0x09 1101=0x0D
0010=0x02 0110=0x06 1010=0x0A 1110=0x0E
0011=0x03 0111=0x07 1011=0x0B 1111=0x0F

上面的例子可以擴充成:

00000001 = 0x01 = 1 (2的0次方)
00000010 = 0x02 = 2 (2的1次方)
00000100 = 0x04 = 4 (2的2次方)
00001000 = 0x08 = 8 (2的3次方)
00010000 = 0x10 = 16 (2的4次方)
00100000 = 0x20 = 32 (2的5次方)
01000000 = 0x40 = 64 (2的6次方)
10000000 = 0x80 = 128 (2的7次方)

ASCII value

電腦裏面所有東西都是用二進制來表示, 每一個字元例如"a", "!", "4" 都有一個數字代表它們。那個數字就是ASCII value。

例如英文字母a, 它的十進制ASCII值是97, 二進制來表示是01100001, 用十六進制來表示是0x61。

表示一個字母就需要8個bit, 即是1個byte。

所以字母b 的ASCII值是98, c 的ASCII值是99...如此類推

所以"abcdefghij"這10個字母拼在一起, 在電腦中儲存的方法是:
01100001 01100010 01100011 01100100 01100101 01100110 01100111 01101000 01101001 01101010

每個字母佔1 byte, 10個字母佔10 bytes:

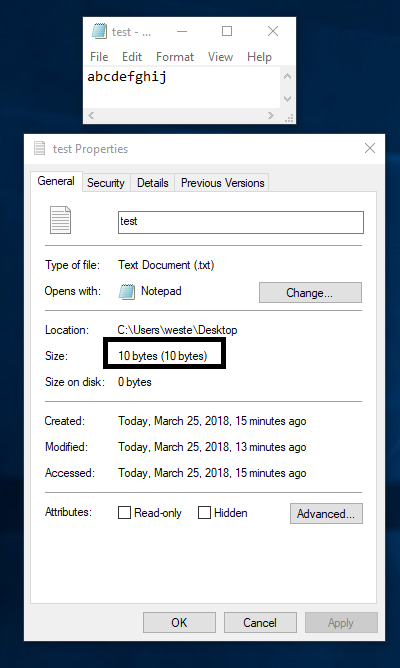
一般情況下懂得ASCII值也沒太大作用, 但如果有一天keyboard 的a 鍵壞了, 你可以按住Alt, 然後按數字鍵盤9和7(注意是先按9然後按7, 不是一齊按, 而且一定是數字鍵盤那邊的數字才可以, 主鍵盤上的數字鍵沒有這個功能), 然後a字就出現了!

透過ASCII value, 我們可以將任意字句轉換成二進制數字, 成為SHA256 Hash function的輸入。

簡單Bitwise Operations: AND/OR/XOR/NOT

Bitwise Operation是電腦CPU最底層的操作, 平常聽到一個CPU 裏面有幾十億個電晶體, 都是為了實現Bitwise Operation。

AND/OR/XOR有兩個輸入bit, 一個輸出bit:

1. AND (與)
0 AND 0 = 0
0 AND 1 = 0
1 AND 0 = 0
1 AND 1 = 1
就是要AND起來的兩個bit都是1, 輸出才是1。

2. OR (或)
0 OR 0 = 0
0 OR 1 = 1
1 OR 0 = 1
1 OR 1 = 1
只要OR起來的兩個bit隨便一個1, 輸出就會是1。

3. XOR (eXclusive Or, 異或)
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0
XOR起來的兩個數一定要不一樣, 輸出才是1。

4. NOT(非)
NOT 1 = 0
NOT 0 = 1
XOR起來的兩個數一定要不一樣, 輸出才是1。

這些Bit Operations可以直接應用到Byte上, 例如:
11 AND 01 = 01
01 OR 10 = 11
11 AND 01 = 10
NOT 0011 = 1100

再複雜一點的例子:
NOT((00001100 OR 11110000) AND 00001111)
= NOT(11111100 AND 00001111)
= NOT(00001100)
= 11110011

複雜的Bitwise Operations: 右移/循環右移/Concatenation/Modular addition

5. Right shift
把所有bit向右移一格, 最左邊的bit變成0。

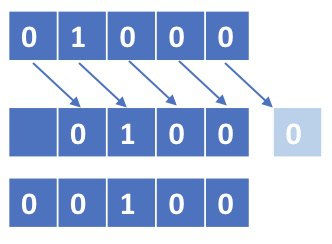
例如:
ShR(10000) = 01000
ShR(01000) = 00100
ShR(00100) = 00010
ShR(00010) = 00001
ShR(00001) = 00000

有時候如果要一次過右移幾次, 可以寫成這樣:
ShR(00110,2) = 00001
意思是把00110右移兩次

6. RotR(circular right shift, 循環右移)
把所有bit向右移一格, 原本最右邊的bit變成第一個bit。

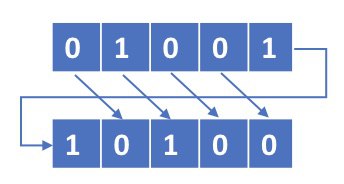
例如:
RotR(10000) = 01000
RotR(01000) = 00100
RotR(00100) = 00010
RotR(00010) = 00001
RotR(00001) = 10000
重覆這個動作, 最終會回到起始數。

再多給幾個例子:
RotR(00110) = 00011
RotR(00011) = 10001

有時候如果要一次過右移幾次, 可以寫成這樣:
RotR(00110, 2) = 10001
意思是把00110循環右移兩次。

7. Concatenation ||
有時候我們需要將兩個二進制數前後並排在一起。
例如: 0011 || 1111 = 00111111

最後一個基本operation
8. Integer addition modulo 2^32, 寫成A+B
如果沒有限制數字長度的話, 其實二進制裏的加法和十進制沒分別。
假設限制了數字長度為1, 在十進制的情況下可以想象成圓圈上有10個點, 分別為0-9

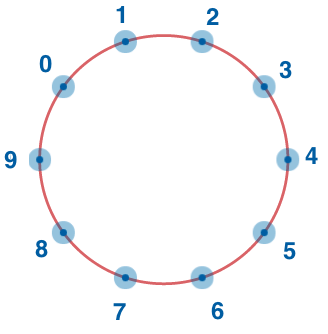
加法就像在圓圈中順時針向前走, +1走一步, +2走兩步
9+1本應=10, 但是因為數字長度有限制, 沒法進位, 所以9+1會回歸原點變0
所以9+1=0, 9+2=1, 7+8=5, 8+3=1

在數論上這種結構可以寫成(a+b) mod n, 在10進制的情況下, n=10
mod n 的意思是除以n之後的餘數, 例如7+8=15, 除10之後的餘數為5, 所以7+8=5

在二進制32位長的數字裏也是這樣:
假設兩個32位出的二進制數相加, 如果結大過2^32, 就要除以2^32, 找出餘數
為甚麼是32位? 因為10年前一般家用電腦在單一cycle裏能處理的二進制數最長只有32位, 超出32位後會overflow。

看以下例子:

上圖中第一個例子, 沒有overflow, 很簡單

第二個例子1111 1111 1111 1111 1111 1111 1111 1111 即是2^32-1, 加上2, 沒有位數限制情況下應該是2^32+1

但2^32+1需要33個bit來表示, 所以要用(2^32+1)/2^32的餘數來表示, 即是1。

SHA256中用到的基本函數:Choose 和 Majority

下面這兩個又AND 又XOR 的是SHA256 中用到的基本函數:
Ch(X, Y, Z) = (X AND Y ) XOR (~X AND Z)
Maj(X, Y, Z) = (X AND Y ) XOR (X AND Z) XOR (Y AND Z)

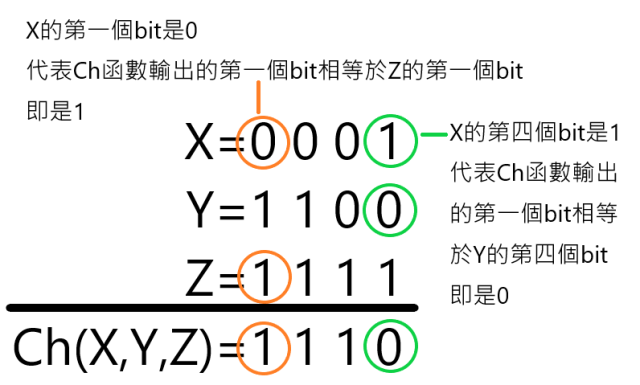
Ch的意思是choose, 如果x 的第i 個bit 是0, 那麼輸出中的第i個bit 與z 的第i 個bit 相等。如果x 的第i 個bit 是1, 那麼輸出中的第i 個bit 與y 的第i 個bit 相等。

看不懂不要緊, 看以下例子:
X = 0001, Y = 1100, Z = 1111
Ch(0001, 1100, 1111)
= (0001 AND 1100) XOR (~0001 AND 1111)
= 0000 XOR (1110 AND 1111)
= 0000 XOR 1110
= 1110

X 的首3個bit都是0, 代表輸出中的首3個bit與z中的首3bit一樣(111)
X 的第4個bit是1, 代表輸出中的第4個bit與y中的第4個bit一樣(0)
所以Ch 的輸出是1110

Maj 的意思是Majority:
如果X/Y/Z 中的第i個bit全都是1, 或者有兩個1, 則輸出中的第i個bit是1
如果X/Y/Z 中的第i個bit全都是0, 或者有兩個0, 則輸出中的第i個bit是0

例子:
X = 0001, Y = 1100, Z = 1111
Maj(X, Y, Z)
= (0001 AND 1100) XOR (0001 AND 1111) XOR (1100 AND 1111)
= 0000 XOR 0001 XOR 1100
= 0001 XOR 1100
= 1101

X/Y/Z 中的第1個bit, 有兩個1, 所以輸出中的第一個bit是1
X/Y/Z 中的第2個bit, 有兩個1, 所以輸出中的第二個bit是1
X/Y/Z 中的第3個bit, 有兩個0, 所以輸出中的第三個bit是0
X/Y/Z 中的第4個bit, 有兩個1, 所以輸出中的第四個bit是1

好啦, 學了這麼多基本operations...

終於可以開始算SHA256啦!

假設我們要計算輸入(M)的SHA256 輸出。
再假設M 的長度剛剛好是512bits的倍數。 先將輸入(M)分為每截512bits, 如果M的長度是5120bits的話, M就會被拆分為10份(m1-m10), 每份的長度均為512bits。

然後每一份m再被切割為16個words (記得1 word = 32 bits, 16 words 剛好等於512bit)
這16個Words 分別叫做W1, W2, W3, W4, W5…, W16
W1||W2||W3||W4||…||W16 就是原本的輸入

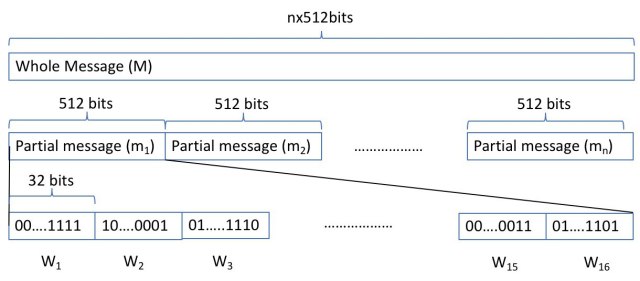
然後還需要多48個附助字節(W17-W64)

W17=[RotR(W15, 17) XOR RotR(W15, 19) XOR ShR(W15, 10)] + W8 + [RotR(W2, 7) XOR RotR(W2, 18) XOR ShR(W2, 3)] + W1

W18=[RotR(W16, 17) XOR RotR(W16, 19) XOR ShR(W16, 10)] + W9 + [RotR(W3, 7) XOR RotR(W3, 18) XOR ShR(W3, 3)] + W2

…..

W64=[RotR(W62, 17) XOR RotR(W62, 19) XOR ShR(W62, 10)] + W57 + [RotR(W49, 7) XOR RotR(W49, 18) XOR ShR(W49, 3)] + W48

用一條式表示:Wi=[RotR(Wi-2, 17) XOR RotR(Wi-2, 19) XOR ShR(Wi-2, 10)] + W-7 + [RotR(Wi-15, 7) XOR RotR(Wi-15, 18) XOR ShR(Wi-15, 3)] + Wi-16, 17 ≤ i ≤ 64

一時間理解不了這部份, 很正常...把一個m切開做16個words還不夠? 還要亂七八糟地堆砌W17-W64有甚麼用?!

這一步叫message expansion, 目的是要混淆嘗試破解SHA256的人。

在沒有W17-W64的情況下, 假設m1裏的最後一個bit反轉了(1變0), 只有W16受影響
在有W17-W64的情況下, W16, W18, W23, W31, W32都會有影響

現在我們將nx512bits的原輸入(M), 切割成n個512bits的m (m1-mn), 每一個m 再變化為64個words (W1-W64)

再定義8個變數H1-H8, 這8個變數的初始值為:
H(0)1 = 0x6a09e667
H(0)2 = 0xbb67ae85
H(0)3 = 0x3c6ef372
H(0)4 = 0xa54ff53a
H(0)5 = 0x510e527f
H(0)6 = 0x9b05688c
H(0)7 = 0x1f83d9ab
H(0)8 = 0x5be0cd19
(其實是頭8個質數的開方根的小數部份的首32bits)

來到最最最複雜的一步!
由m1到mn, 每一個m 都要做以下的運算:

– set (a, b, c, d, e, f, g, h) = (H(t−1)1, H(t−1)2, H(t−1)3, H(t−1)4, H(t−1)5, H(t−1)6, H(t−1)7, H(t−1)8)

– do 64 rounds consisting of:
T1 = h + [RotR(e, 6) XOR RotR(e, 11) XOR RotR(e, 25)] + Ch(e, f, g) + Ki + Wi
T2 = [RotR(a, 2) XOR RotR(a, 13) XOR RotR(a, 22)] + Maj(a, b, c)
h = g
g = f
f = e
e = d + T1
d = c
c = b
b = a
a = T1 + T2

Ki 是另一堆常數
t 是指現在運算的是第幾個m, 例如m1 的話, t 就是1
i 是指現在到64 round中的第幾round

當m1 的64round 運算完畢, 我們會得到一堆a,b,c,d,e,f,g,h

再用下面這一組算式更新H 的值, 新的H 就是計算m2 時的H 的初始值:

H(t)1 = H(t−1)1 + a
H(t)2 = H(t−1)2 + b
H(t)3 = H(t−1)3 + c
H(t)4 = H(t−1)4 + d
H(t)5 = H(t−1)5 + e
H(t)6 = H(t−1)6 + f
H(t)7 = H(t−1)7 + g
H(t)8 = H(t−1)8 + h

所以完成運算m1 部份後會得到:
H(1)1, H(1)2, H(1)3, H(1)4, H(1)5, H(1)6, H(1)7, H(1)8

這堆H會成為運算m2時的H的初始值, 一直運算到mn之後會得出:
H(n)1, H(n)2, H(n)3, H(n)4, H(n)5, H(n)6, H(n)7, H(n)8

最後將這8個H concatenate 在一起就是SHA256 的輸出值了!!

SHA256(M) = H = H(N)1||H(N)2||H(N)3||H(N)4||H(N)5||H(N)6||H(N)7||H(N)8

參考: https://helix.stormhub.org/papers/SHA-256.pdf
https://csrc.nist.gov/csrc/media/publications/fips/180/4/final/documents/fips180-4-draft-aug2014.pdf

---

延伸閱讀